알고리즘 풀이 링크
Greedy (탐욕법)
각 단계마다 지금 당장 가장 좋은 방법만을 선택하는 해결 방법
- 동적 계획법보다 수행 시간이 훨씬 빠르다
- 문제 유형을 바로 파악할 수 없는 경우 그리디 알고리즘을 의심
- 기준에 따라 좋은 것을 선택하므로 '가장 큰 순서대로'와 같은 기준을 제시
- 정렬 알고리즘과 같이 출제되는 경향
최적해를 찾을 수 있는 두 가지 조건
1) 탐욕법을 사용해도 항상 최적해를 구할 수 있는 경우
2) 시간, 공간적 제약으로 최적해 대신 근사해를 찾아서 해결하는 경우
Greedy의 특성
1) 탐욕적 선택 속성 : 항상 각 단계에서 우리가 선택한 답을 포함하는 최적해가 존재하는가?
2) 최적 부분 구조 : 각 단계에서 항상 최적의 선택만을 했을 때, 전체 최적해를 구할 수 있는가?
import Foundation
var input = readLine()!.components(separatedBy:" ").map{Int($0)!}
var input2: [Int] = []
for _ in (0..<input[0]) {
input2.append(Int(readLine()!)!)
}
var count: Int = 0
var n = input[1]
for coin in input2.reversed() {
count += n / coin
n %= coin
}
print(count)
구현 문제
- 풀이를 떠올리는 것은 쉽지만 코드로 옮기기 어려운 문제
- 길어지는 소스코드, 특정 소수점 자리 출력, 문자열 파싱 등
- 완전 탐색 : 모든 경우의 수를 다 계산하는 해결 방법
- 시뮬레이션 : 문제에서 제시한 알고리즘을 한 단계씩 차례대로 수행 (ex. 좌표 이동)
- 코딩 테스트에서 그리디 알고리즘과 함께 1, 2번 단골 출제
- 그리디 알고리즘과 묶어서 출제되는 경향
DFS/BFS
DFS(Depth First Search, 깊이 우선 탐색)
- 필요한 개념 : 재귀 함수, 그래프
- 일반적으로는 번호가 낮은 노드부터 처리하는 것이 관행
- 데이터의 개수가 N개인 경우 O(N)의 시간이 소요
- 스택을 이용하므로 실제 구현은 재귀 함수를 이용했을 때 간결하게 구현 가능
구체적인 동작 과정
1) 탐색 시작 노드를 스택에 삽입 후 방문 처리
2) 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면, 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냄
3) 2번의 과정을 더 이상 수행할 수 없을 때까지 반복
// DFS 메서드 정의
func dfs(_ graph: [[Int]], _ v: Int, _ visited: inout [Bool]) {
visited[v] = true
print("\(v)")
for i in graph[v] {
if !visited[i] {
dfs(graph, i, &visited)
}
}
}
// 그래프 정보
let graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1,7]
]
// 방문 정보
var visited: [Bool] = Array(repeating: false, count: 9)
dfs(graph, 1, &visited)BFS(Breadth First Search, 너비 우선 탐색)
- 필요한 개념 : 큐
- 일반적인 경우 DFS보다 수행 시간이 빠름
구체적인 동작 과정
1) 탐색 시작 노드를 큐에 삽입하고 방문 처리
2) 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
3) 2번의 과정을 더 이상 수행할 수 없을 때까지 반복
// BFS 메서드 정의
func bfs(_ graph: [[Int]], _ v: Int, _ visited: inout [Bool]) {
var queue: [Int] = [v]
var v = v
visited[v] = true
while !queue.isEmpty {
v = queue.removeFirst()
print("\(v)")
for i in graph[v] {
if !visited[i] {
queue.append(i)
visited[i] = true
}
}
}
}
// 그래프 정보
let graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1,7]
]
// 방문 정보
var visited: [Bool] = Array(repeating: false, count: 9)
bfs(graph, 1, &visited)정렬 알고리즘(Sorting)
- 미리 만들어진 라이브러리를 사용하는 것이 효과적인 경우가 많음
- 정렬 알고리즘 문제는 외워서 잘 풀어낼 수 있는 문제
Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Heap Sort, Quick Sort
Bubble Sort
가장 큰 값을 배열의 맨 끝에다 이동시키면서 정렬하고자 하는 원소의 개수 만큼을 두 번 반복하게 됨.
| 실행 시간의 상한 | 실행 시간의 하한 |
|---|---|
| O(n^2) | O(n^2) |
for i in 0..<list.count {
for j in 0..<list.count - i - 1 {
if list[j] > list[j + 1] {
let temp = list[j]
list[j] = list[j + 1]
list[j + 1] = temp
}
}
}Selection Sort
가장 작은 데이터를 선택해 첫 번째 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 두 번째 데이터와 바꾸는 정렬 방법.
| 실행 시간의 상한 | 실행 시간의 하한 |
|---|---|
| O(n^2) | O(n^2) |
for i in 0..<list.count {
var minValue = 999
var index = 0
for j in i..<list.count {
if list[j] < minValue {
minValue = list[j]
index = j
}
}
var temp = list[i]
temp = list[i]
list[i] = minValue
list[index] = temp
}이진 탐색(Binary Search)
- 배열 내부의 데이터가 정렬되어있어야 사용 가능
- 단계를 거칠 때마다 확인하는 원소가 평균적으로 절반으로 줄어듦
- 시간 복잡도 : O(logN)
- 반복적, 재귀적 두 가지 방법으로 구현 가능
- 탐색 범위가 큰 경우 이진 탐색으로 접근
while startIndex <= endIndex {
if list[middleIndex] == value {
index = middleIndex
break
}
if list[middleIndex] > value {
startIndex = middleIndex + 1
} else if list[middleIndex] < value {
endIndex = middleIndex - 1
}
}다이나믹 프로그래밍(DP, Dynamic Programming)
- 복잡한 문제를 여러 개의 하위 문제로 나누어 메모리를 사용하는 대신 시간을 줄이는 방법.
- 완전 탐색으로 접근했을 때 시간이 오래걸리는 경우 적용 가능한지 확인
- 코딩 테스트에서는 대체로 간단한 형태로 출제
- DP 테이블 : 보텀업(bottom-up) 방식에서 사용되는 결과 저장용 리스트
- 메모이제이션(Memoization) : 탑다운(top-down) 방식에서 사용되는 이전에 계산된 결과를 일시적으로 저장해놓는 리스트
DP를 사용할 수 있는 조건
1) 큰 문제를 작은 문제들로 나눌 수 있다.
2) 작은 문제에서 구한 정답이 큰 문제에서도 사용된다.
DP 구현 방식 2가지
1) 보텀업(bottom-up) 방식
- 작은 문제부터 차근 차근 답을 도출하는 방식
- 반복문 형태
- 다이나믹 프로그래밍의 전형적인 형태
// DP 테이블
var d = Array(repeating:0, count:100)
d[1] = 1
d[2] = 1
let n = 99
for i in 3..<n+1 {
d[i] = d[i-1] + d[i-2]
}2) 탑다운(top-down) 방식
- 큰 문제를 해결하기 위해 작은 문제를 해결하는 방식
- 재귀함수 형태
- 값이 중복되더라도 함수를 사용하는데 드는 오버헤드가 발생하므로 보텀업 방식이 더 효율적
var d = Array(repeating:0, count:100)
func fibo(_ x: Int) -> Int {
if x == 1 || x == 2 {
d[x] = 1
return 1
}
if d[x] != 0 {
return d[x]
}
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
}분할 정복(Divide and Conquer)
- 큰 문제를 작은 문제로 쪼개어 답을 찾는 방식, 탑다운(top-down) 접근법 사용
- 하부구조가 반복되지 않는 문제를 해결할 때 사용
- DP와의 차이점 : 다이나믹 프로그래밍들의 문제들은 서로 영향을 미침(overlapping)
접근 방법
DP vs Divide and Conquer vs Greedy
| Divide and Conquer | Dynamic Programming | Greedy |
|---|---|---|
| non-overlapping한 문제를 작은 문제로 쪼개어 해결하는데 non-overlapping | overlapping substructure를 갖는 문제를 해결한다. | 각 단계에서의 최적의 선택을 통해 해결한다. |
| top-down 접근 | top-down, bottom-up 접근 | |
| 재귀 함수를 사용한다. | 재귀적 관계(점화식)를 이용한다.(점화식) | 반복문을 사용한다. |
| call stack을 통해 답을 구한다. | look-up-table, 즉 행렬에 반복적인 구조의 solution을 저장해 놓는 방식으로 답을 구한다. | solution set에 단계별 답을 추가하는 방식으로 답을 구한다. |
| 분할 - 정복 - 병합 | 점화식 도출 - look-up-table에 결과 저장 - 나중에 다시 꺼내씀 | 단계별 최적의 답을 선택 - 조건에 부합하는지 확인 - 마지막에 전체조건에 부합하는지 확인 |
| 이진탐색, 퀵정렬, 합병정렬 | 최적화 이진탐색, 이항계수 구하기, 플로이드-와샬 | 크루스칼, 프림, 다익스트라, 벨만-포드 |
스위프트 자료구조
스택(Stack), LIFO
- 리스트와 메소드를 사용해서 구현 가능
| 연산 | 리스트 메소드 | * 비고 |
|---|---|---|
| push() | append() | |
| pop() | removeLast(), popLast() | popLast()는 빈 배열일 때 nil값을 return |
큐(Queue), FIFO
- 리스트와 메소드를 사용해서 구현 가능
- 출구가 왼쪽, 입구가 오른쪽인 큐 형태를 가지게 됨
| 연산 | 리스트 메소드 |
|---|---|
| enqueue() | append() |
| dequeue() | removeFirst() |
그래프(Graph)
- 노드(Node)들이 간선(Edge)으로 연결되어있는 구조
- 두 노드가 간선으로 연결되어있다면 인접하다.
- 탐색 문제를 보면 그래프로 바꿔서 생각해보기
프로그래밍 언어에서의 구현
1) 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현
- 모든 관계를 저장하므로 메모리가 낭비됨
- 그러나 특정 노드간의 연결 관계를 찾는데 유리
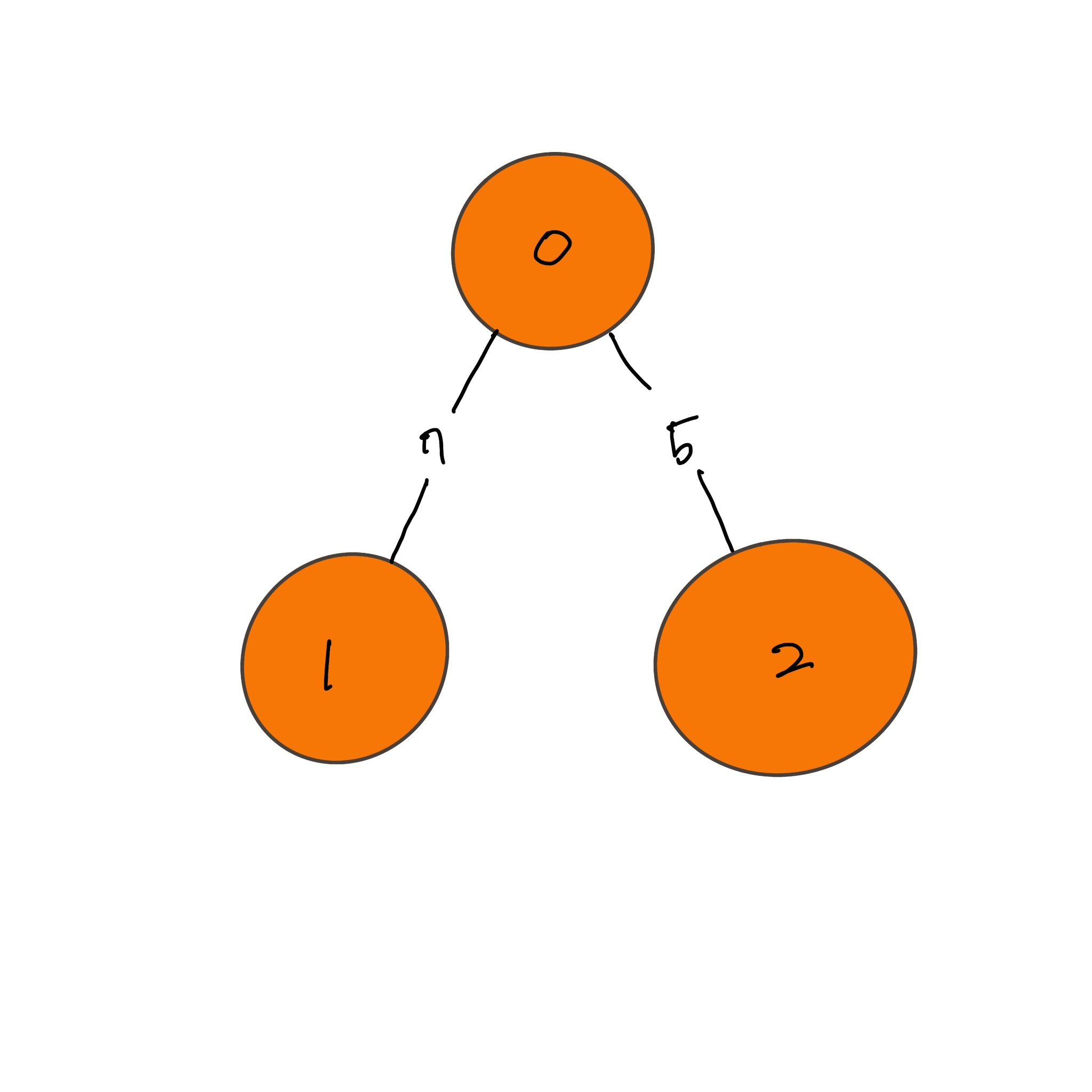
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0 | 7 | 5 |
| 1 | 7 | 0 | 무한 |
| 2 | 5 | 무한 | 0 |
let INF = 9999999 // 연결되지 않음을 표현
// 2차원 리스트를 이용한 인접 행렬 표현
let graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]2) 인접 리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현
- 특정한 노드와 인접한 노드를 순회하는 경우 메모리 공간의 낭비가 적음
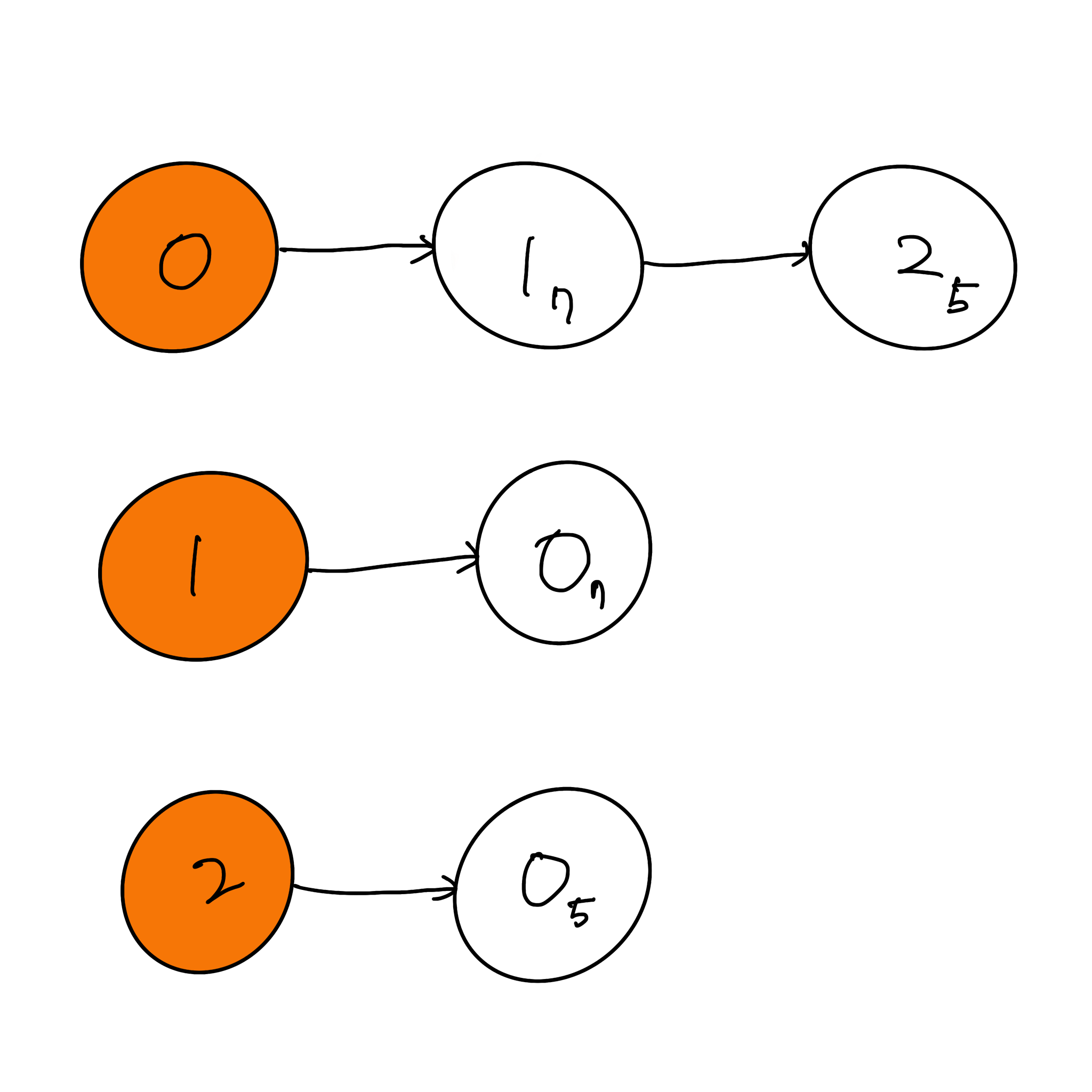
// 행이 3개인 2차원 리스트 생성
var graph: [[(Int, Int)]] = Array(repeating: Array(repeating: (0, 0), count: 0), count: 3)
// 노드 0에 연결된 노드 정보 저장 (노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
// 노드 1에 연결된 노드 정보 저장 (노드, 거리)
graph[0].append((0, 7))
// 노드 2에 연결된 노드 정보 저장 (노드, 거리)
graph[0].append((0, 5))
// 출력 : [[(1, 7), (2, 5), (0, 7), (0, 5)], [], []]트리(Tree)
- 사이클(Cycle)이 존재하지 않는 그래프
- 이진 탐색 트리 : 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
필수 개념
재귀 함수(Recursive Function)
- 내부적으로 스택을 사용
- 스택을 사용하는 많은 알고리즘은 재귀를 통해 간편하게 구현될 수 있음, 대표적으로 DFS
재귀 함수의 필요 조건
1) 점화식 : 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것
2) 종료 조건 : 재귀를 언제 끝마칠 것인지에 대한 조건 (return 조건)
1) 팩토리얼을 반복적으로 계산한 경우
func factorial(_ n: Int) -> Int {
var result = 1
for i in 1...n {
result *= i
}
return result
}2) 팩토리얼을 재귀적으로 계산한 경우
func factorial_recursive(_ n: Int) -> Int {
if n == 1 {
return 1
}
return n * factorial_recursive(n-1)
}
참고 링크
Interview_Question_for_Beginner
이것이 코딩테스트다 - 한빛 미디어(나동빈 저)
댓글